01
van 05
Babylonische nummers
Drie hoofdgebieden van verschil met onze nummers
Aantal symbolen gebruikt in Babylonische wiskunde
Stel je voor hoeveel gemakkelijker het zou zijn om in de beginjaren rekenen te leren als je alleen maar een regel als ik en een driehoek moest leren schrijven. Dat is eigenlijk alles wat de oude mensen van Mesopotamië moesten doen, hoewel ze ze hier en daar varieerden, verlengen, draaien, enz.
Ze hadden onze pennen en potloden of papier trouwens niet. Wat ze schreven was een hulpmiddel dat je in de beeldhouwkunst zou gebruiken, omdat het medium klei was. Of dit moeilijker of gemakkelijker te leren is dan een potlood, is een gooi, maar tot nu toe staan ze voor op de afdeling gemak, met slechts twee basissymbolen om te leren.
Basis 60
De volgende stap gooit een sleutel naar de afdeling eenvoud. We gebruiken een Basis 10, een concept dat voor de hand lijkt te liggen aangezien we 10 cijfers hebben. We hebben er eigenlijk 20, maar laten we aannemen dat we sandalen dragen met beschermende teenbekleding om het zand binnen te houden de woestijn, heet van dezelfde zon die de kleitabletten zou bakken en ze voor ons zou bewaren om millennia te vinden later. De Babyloniërs gebruikten deze basis 10, maar slechts gedeeltelijk. Voor een deel gebruikten ze Base 60, hetzelfde aantal dat we overal om ons heen zien in minuten, seconden en graden van een driehoek of cirkel. Ze waren ervaren astronomen en dus zou het aantal afkomstig kunnen zijn van hun waarnemingen van de hemel. Base 60 heeft ook verschillende handige factoren die het gemakkelijk maken om mee te rekenen. Toch is het intimiderend om Base 60 te moeten leren.
In "Hommage aan Babylonië" [The Mathematical GazetteVol. 76, nr. 475, "The Use of the History of Mathematics in the Teaching of Mathematics" (Mar., 1992), pp. 158-178], zegt schrijver-leraar Nick Mackinnon dat hij Babylonische wiskunde gebruikt om 13-jarigen te onderwijzen over andere bases dan 10. Het Babylonische systeem gebruikt base-60, wat betekent dat het niet decimaal is, maar sexagesimaal.
Positionele notatie
Zowel het Babylonische getalsysteem als het onze vertrouwen op positie om waarde te geven. De twee systemen doen het anders, mede omdat hun systeem een nul miste. Het leren van het Babylonische positioneringssysteem van links naar rechts (van hoog naar laag) voor de eerste kennismaking met elementaire rekenkunde is waarschijnlijk niet meer moeilijker dan het leren van onze 2-directionele, waarbij we de volgorde van de decimale getallen moeten onthouden - oplopend van de decimaal, enen, tientallen, honderden, en dan uitwaaieren in de andere richting aan de andere kant, geen enkele kolom, slechts tienden, honderdsten, duizendsten, etc.
Ik zal op verdere pagina's ingaan op de standpunten van het Babylonische systeem, maar eerst zijn er enkele belangrijke getallenwoorden om te leren.
Babylonische jaren
We praten over periodes van jaren met decimale hoeveelheden. We hebben een decennium voor 10 jaar, een eeuw voor 100 jaar (10 decennia) of 10 X 10 = 10 jaar in het kwadraat, en een millennium voor 1000 jaar (10 eeuwen) of 10 X 100 = 10 jaar in blokjes. Ik ken geen hogere term dan dat, maar dat zijn niet de eenheden die de Babyloniërs gebruikten. Nick Mackinnon verwijst naar een tablet van Senkareh (Larsa) van Sir Henry Rawlinson (1810-1895) * voor de eenheden die de Babyloniërs gebruikten en niet alleen voor de betrokken jaren, maar ook voor de geïmpliceerde hoeveelheden:
- soss
- ner
- sar.
sossnersosssarsoss
Nog steeds geen tie-breaker: het is niet per se gemakkelijker om de afgeleide termen uit het kwadraat en het blokje te leren van het Latijn dan zijn het Babylonische lettergrepen met één lettergreep die geen kubusvorming, maar vermenigvuldiging met 10.
Wat denk je? Zou het moeilijker zijn geweest om de basisbeginselen van het getal te leren als een Babylonische schoolkind of als een moderne student op een Engelssprekende school?
* George Rawlinson (1812-1902), Henry's broer, toont een vereenvoudigde getranscribeerde tabel met vierkanten in De zeven grote monarchieën van de oude oosterse wereld. De tabel lijkt astronomisch te zijn, gebaseerd op de categorieën van Babylonische jaren.
Alle foto's zijn afkomstig van deze online gescande versie van een 19e-eeuwse editie van George Rawlinson De zeven grote monarchieën van de oude oosterse wereld.02
van 05
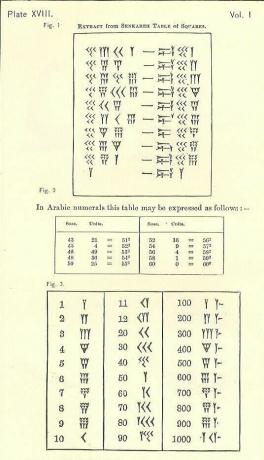
De nummers van Babylonische wiskunde
Sinds we zijn opgegroeid met een ander systeem, zijn Babylonische cijfers verwarrend.
In ieder geval lopen de cijfers van hoog naar links naar laag aan de rechterkant, zoals ons Arabische systeem, maar de rest zal waarschijnlijk onbekend lijken. Het symbool voor een is een wig of Y-vorm. Helaas vertegenwoordigt de Y ook een 50. Er zijn een paar afzonderlijke symbolen (allemaal gebaseerd op de wig en de lijn), maar alle andere nummers worden daaruit gevormd.
Onthoud dat de vorm van schrijven is spijkerschrift of wigvormig. Door de tool die gebruikt wordt om de lijnen te tekenen is er een beperkte variatie. De wig kan al dan niet een staart hebben, getrokken door de spijkerschrift-schrijfpen langs de klei te trekken na het opdrukken van de deeldriehoek.
De 10, beschreven als een pijlpunt, lijkt een beetje op
Drie rijen van maximaal 3 kleine 1's (geschreven als Y's met een aantal verkorte staarten) of 10 seconden (een 10 wordt geschreven als
03
van 05
1 rij, 2 rijen en 3 rijen
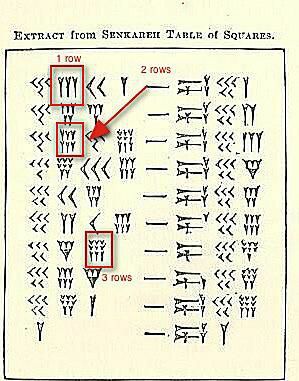
Er zijn drie sets spijkerschriftnummer clusters gemarkeerd in de bovenstaande afbeelding.
Op dit moment zijn we niet bezorgd over hun waarde, maar om te laten zien hoe je 4 tot 9 van hetzelfde nummer gegroepeerd zou zien (of schrijven). Drie gaan achter elkaar. Als er een vierde, vijfde of zesde is, gaat het hieronder. Als er een zevende, achtste of negende is, heb je een derde rij nodig.
De volgende pagina's gaan verder met instructies voor het uitvoeren van berekeningen met het Babylonische spijkerschrift.
04
van 05
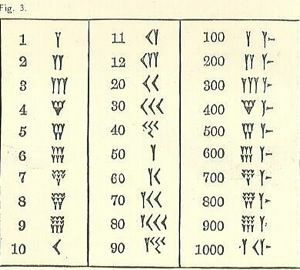
De tabel met vierkanten
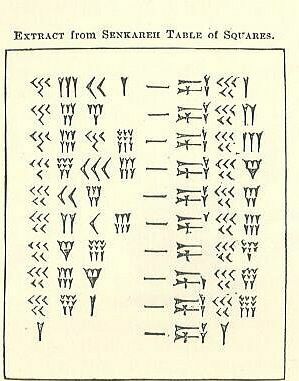
Van wat je hierboven hebt gelezen over de soss - die je je herinnert, is de Babylonische voor 60 jaar, de wig en de pijlpunt - dat zijn beschrijvende namen voor spijkerschrifttekens, kijk of je kunt achterhalen hoe deze berekeningen werken. De ene kant van het streepje is het nummer en de andere is het vierkant. Probeer het als een groep. Als je er niet uitkomt, kijk dan naar de volgende stap.
05
van 05
Hoe de tabel met vierkanten te decoderen

Kun je het nu uitzoeken? Geef het een kans.
...
Er zijn 4 duidelijke kolommen aan de linkerkant, gevolgd door een streepvormig teken en 3 kolommen aan de rechterkant. Kijkend naar de linkerkant, is het equivalent van de 1s-kolom eigenlijk de 2 kolommen die het dichtst bij het "streepje" (binnenkolommen) staan. De andere 2 buitenste kolommen worden samen geteld als de kolom uit de jaren 60.
- De 4-
- De 3-Ys = 3.
- 40+3=43.
- Het enige probleem hier is dat er een ander nummer achter staat. Dit betekent dat ze geen eenheden zijn (de plaats van degenen). De 43 is geen 43-en maar 43-60's, omdat het het sexagesimal (base-60) -systeem is en het zit in de soss kolom zoals de onderste tabel aangeeft.
- Vermenigvuldig 43 met 60 om 2580 te krijgen.
- Voeg het volgende nummer toe (2-
- Je hebt nu 2601.
- Dat is het kwadraat van 51.
De volgende rij heeft 45 in de soss kolom, dus vermenigvuldig je 45 met 60 (of 2700), en tel dan de 4 uit de eenhedenkolom op, dus je hebt 2704. De wortel van 2704 is 52.
Kun je erachter komen waarom het laatste getal = 3600 (60 in het kwadraat)? Hint: waarom is het niet 3000?